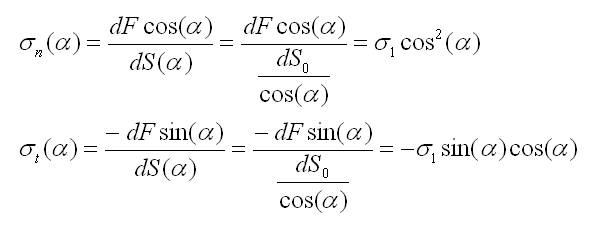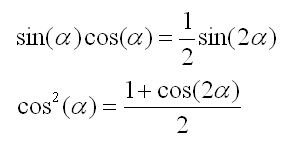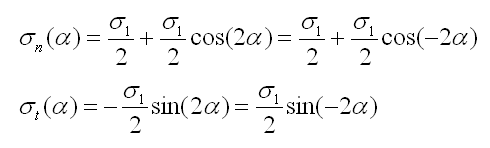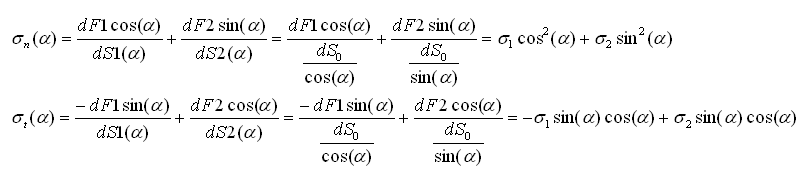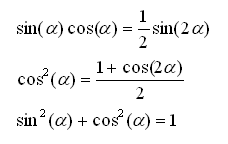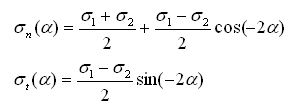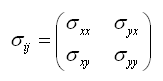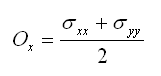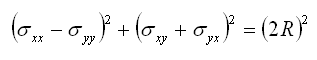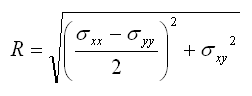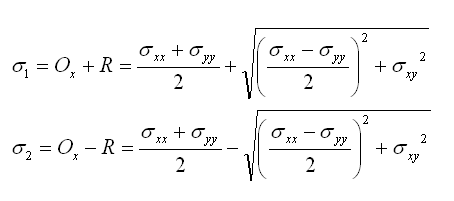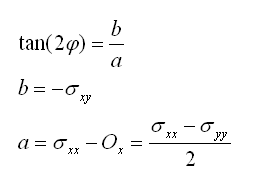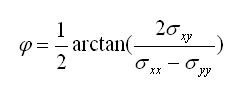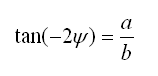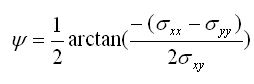Le cercle de Mohr est une représentation en deux dimensions des états de contrainte en un point P du matériau. Cette représentation graphique (cercles ou diagramme de Mohr) a été proposé en 1882 par Christian Otto Mohr.
Notez que pour des efforts non-uniaxiaux on compte plusieurs cercles sur le diagramme.
Utilité
Le diagramme de Mohr est contruit à partir de la connaissance des efforts extérieurs auxquels est soumis le matériau. Il sert ensuite à déterminer
- les contraintes principales et direction principales
- la direction pour laquelle la contrainte de cisaillement est maximale ainsi que sa valeur.
La direction de contrainte de cisaillement maximale correspond généralement au plan de rupture fragile du matériau.
Fondements mathématiques de la représentation de Mohr
Cas d'une solicitation unidimensionnelle
On considère un élément de volume autour d'un point P du matériau, cet élément subi une force F dans la direction x (cf. shéma ci-dessous). La contrainte σx dans la direction x correspond alors à la composante principale σ1.
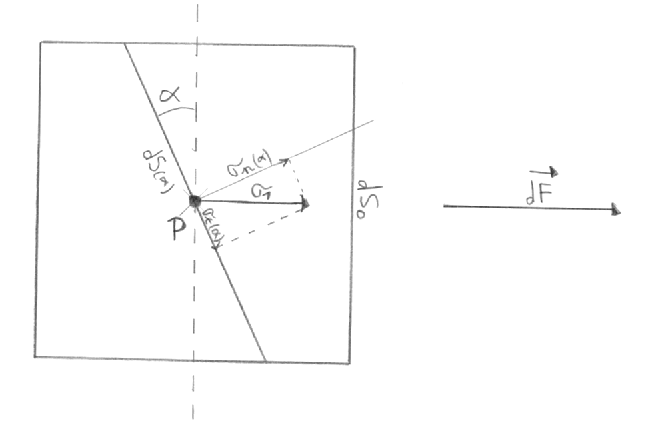
On prépare un graphe avec en abscisse la contrainte normale et en ordonnée la contrainte tangentielle par rapport divers plans que l'on va choisir maintenant.
On va considérer tout une série de plan faisant un angle α, allant de 0 à π, avec la direction x. Pour chaque plan (donc pour chaque α) on trace sur le graphe un point aux coordonnées (σn(α), σt(α)).
La forme mathématique pour σn et σt en fonction de α est la suivante:
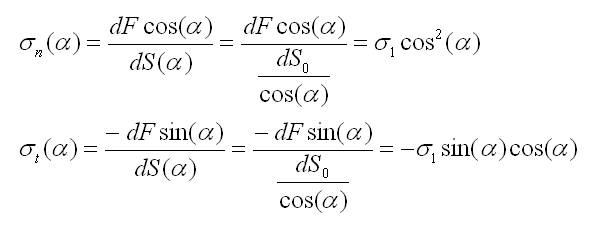
On utilise ensuite les identités trigonométriques suivantes:
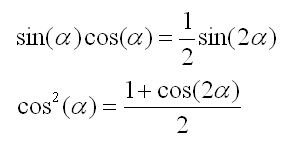
et on obtient les deux relations:
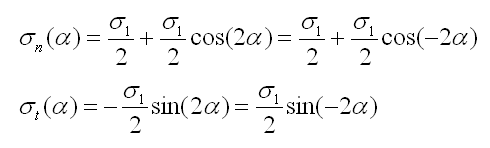
On reconnait alors l'équation paramétrique d'un cercle, centré en (σ1/2 , 0) et de rayon σ1/2.
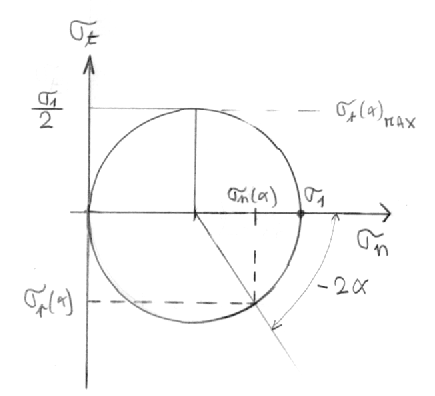
Notez que lorsque le plan tourne d'un angle α dans l'espace physique, on se déplace d'un angle -2α sur le cercle de Mohr.
La contrainte tangentielle maximale σt,max est égale à σ1/2 et elle intervient pour une orientation correspondant à 2α = π/2, soit alpha = 45°.
Cas d'une solicitation bidimensionnelle
On considère un élément de volume autour d'un point P du matériau, cet élément subi des contraintes dans un plan (x,y).
On sait qu'il existe des directions principales pour lesquelles les composantes tangentielles du tenseur de contrainte sont nulles. Choisissons alors de représenter notre élément de volume autour du point P dans ce système de coordonnée défini par les directions principales. Dans le shéma ci-dessous on représente les composantes dues à la première contrainte principale et celles dues à la deuxième contrainte principale sur deux shémas séparés afin de rendre le tout plus lisible. La représentation globale consite à la supperposition de ces deux shémas:
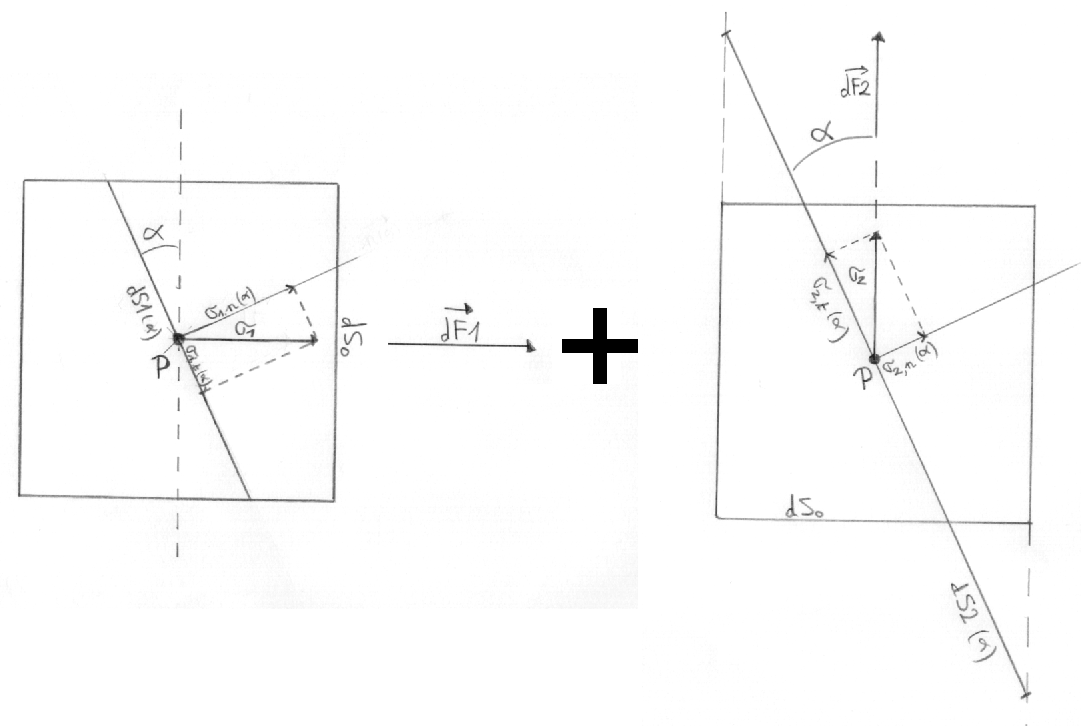
Comme précédemment on choisi un plan qui fait un angle alpha avec x (première direction principale). Les composantes normales et tangentielles, σn(α) et σt(α), par rapport à ce nouveau plan sont donc:
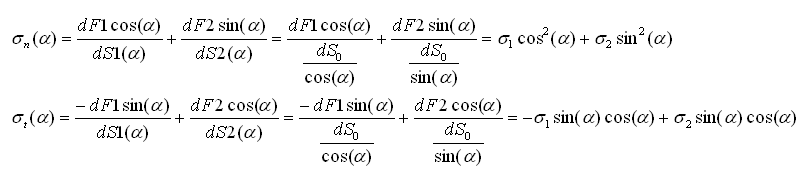
En utilisant les relations géométriques:
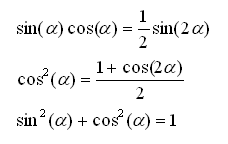
on réécrit les égalités de la manière suivante:
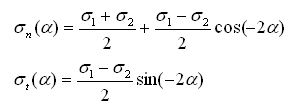
On reconnait alors l'équation paramétrique d'un cercle, centré en [(σ1+σ2)/2 , 0] et de rayon (σ1-σ2)/2.
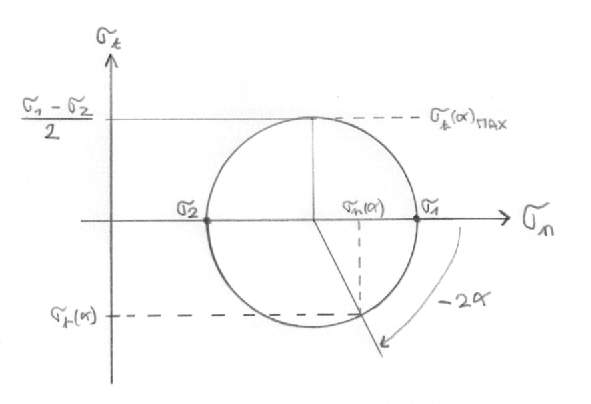
La contrainte tangentielle maximale σt,max est égale à (σ1-σ2)/2 et elle intervient pour une orientation correspondant à 2α = π/2, soit pour un plan présentant un angle de 45° par rapport à la première direction principale.
Construction des cercles et déductions pratiques
On considère le cas d'une solicitation bidimensionnelle (le cas unidimensionnel en est un cas particulier).
Construction du cercle de Mohr
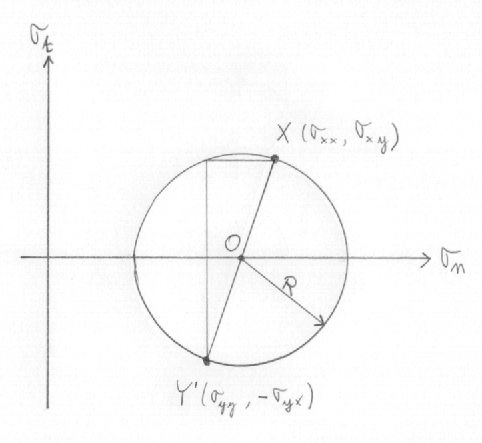
A partir de la connaissance de l'état de contrainte exprimé dans n'importe quel système de coordonnée cartésien (x,y) on peut construire le cercle de Mohr.
Dans la notation matricielle habituelle l'état de contrainte dans le système (x,y) est:
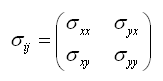
Pour construire le cercle de Mohr on commence par tracer les axes σn et σt. Puis on ajoute les points X(σxx, σxy) et Y'(σyy, -σyx). L'intersection entre le segment [XY'] et l'abscisse correspond au centre du cercle O.
La position sur l'abscisse du centre du cercle est donc:
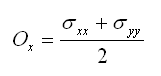
En appliquant le théorème de Pythagore et en notantant R le rayon du cercle de Mohr on peut écrire la relation:
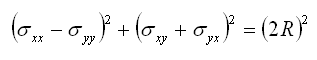
en considérant la symétrie du tenseur des contraintes (σij = σji) et en isolant R, on en déduit le rayon du cercle de Mohr:
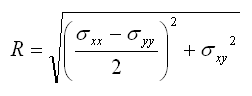
Ce que l'on peut déduire du cercle de Mohr
Voici d'abord un petit shéma qui permettra de bien définir les termes et faciliter le raisonnement:
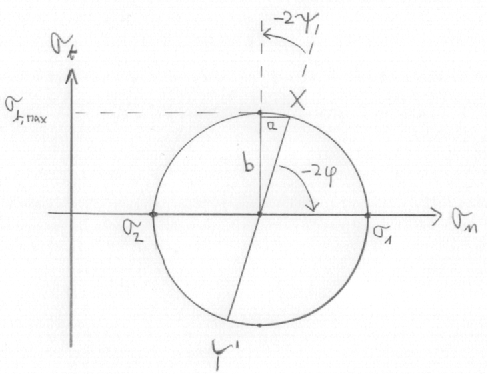
Contrainte normale maximale et minimale:
Les valeurs extremales pour la contrainte normale interviennent lorsque le cercle coupe l'abscisse. Les contraintes tangentielles sont alors nulles, ces contraintes normales maximales et minimales correspondent donc au contraintes principales σ1 et σ2. Leur valeur en fonction de σij est
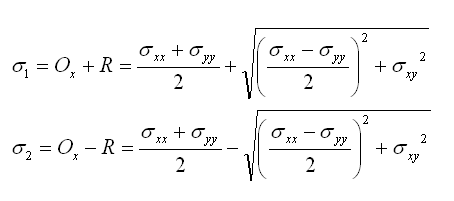
Angle entre le plan de contrainte normale maximale et x:
Pour rappelle, l'angle parcouru sur le cercle de Mohr correspond à l'inverse du double de l'angle réel entre les deux plans considérés. Les relations trigonométriques usuelles nous donnent donc la relation suivante:
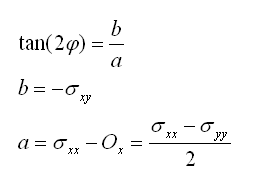
D'où la formule pour exprimer l'angle entre le plan x et le plan correspondant à la contrainte normale maximale σ1:
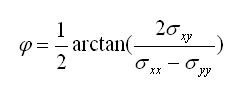
Contrainte tangentielle (cisaillement) maximale et minimale:
Les contraintes de cisaillement sont maximales, respectivement minimales, pour les plans orientés à 90° des plans correspondants aux axes principaux. Les valeurs de cisaillement maximale et minimale sont R et -R.
On a vu ci-dessus que dans le repère cartésion quelconque (x,y) la valeur de R s'écrit:
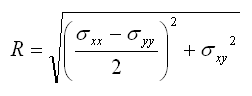
Angle entre le plan de contrainte tangentielle maximale et x:
Les relations trigonométriques usuelles nous donnent la relation suivante:
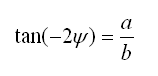
D'où la formule pour exprimer l'angle entre le plan x et le plan correspondant à la contrainte de cisaillement maximale σxy, max:
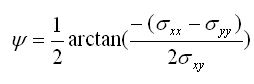
|