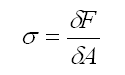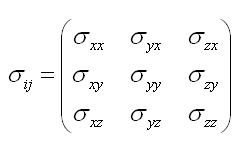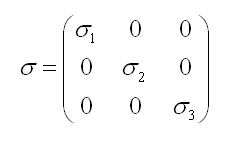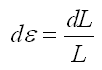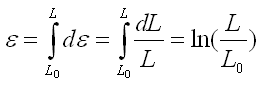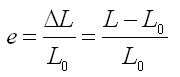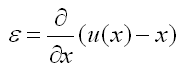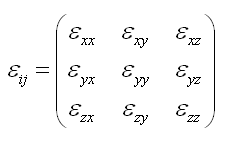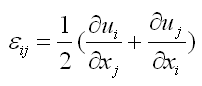Comportement mécanique des matériaux - Contraintes et déformations |
ContraintesLa contrainte est définie comme l'intensité de force à un point donnée du matériau. Sur une surface infinitésimale on a donc:
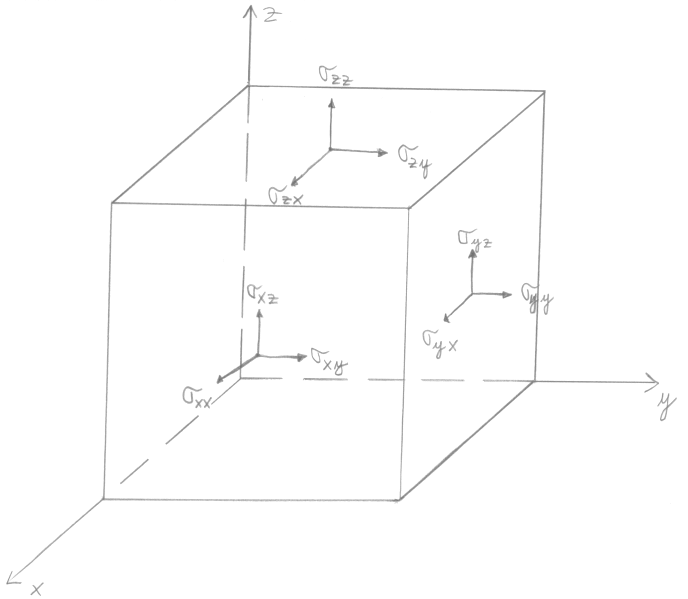
Lorsque la surface est normale à la surface on parle de contrainte normale. Lorsque la force est parallèle à la surface on a affaire à une contrainte de cisaillement. Dans le cas général l'état de contrainte sur un élément infinitésimal du matériau est décrit par une tenseur à neufs composants.
Ce tenseur est symétrique σij = σji sinon l'élément de volume subirait une accélération illimitée en rotation. Donc six des composants du tenseur des contraintes σ sont réellement indépendants. Le premier indice représente la normale à la surface considérée. Le second indice correspond à la direction de la force sur la surface en question.
Si le tenseur σij n'était pas symétrique la somme des moments ne serait pas nulle et le volume subirait une accélération infinie de rotation. L'une des propriétés d'un tenseur symétrique est d'être diagonalisable. Autrement dit, on peut toujours trouver un système de coordonnées pour lequel le tenseur des contraintes est représenté par une matrice diagonale:
σ1 σ2 et σ3 sont appellées contraintes principales et 1,2,3 sont les axes principaux de contrainte.
Déformations locales (strains)La déformation locale normalisée dans un volume soumis à de contraintes est généralement notée ε. Elle représente la variation dans les positions relatives entre points voisins du matériau.
Cas unidimensionnel Au niveau infinitésimal et unidimensionnel la déformation locale est définie par la variation de longueur L:
Lors d'un processus d'élongation d'une longueur L0 à L la déformation naturelle est alors l'intégrale:
Le nom courant utilisé dans la littérature anglaise est true strain, logarithmic strain or Hencky strain. On défini également la déformation nominale (ou ingénieur) par la relation:
On en déduit la relation:
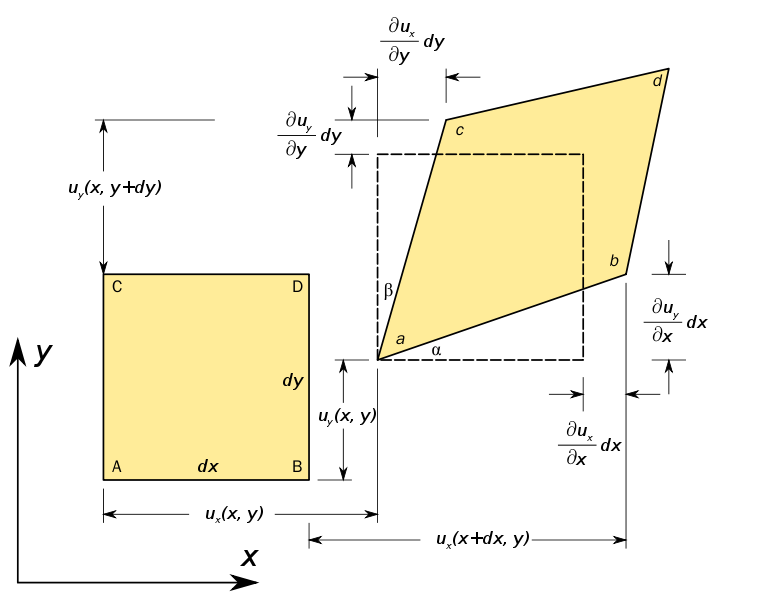
Généralisation De manière générale lorsqu'un volume subi une déformation au niveau macroscopique chaque position x dans le volume est transformé en une nouvelle position x' = u(x).
La déformation locale est alors définie par:
En considérant le cas des petites déformations ε peut être traité comme un tenseur:
Comme le tenseur des contraintes, celui des déformations locales est symétrique εij = εji. |